LoRA Without Regret

Thinking Machines have been posting a remarkable stream of blog posts lately, genuinely practical, surprisingly accessible, and directly applicable for all practitioners. They're stuff has been very hands on, garnering a lot of positive community sentiment. The post I’m covering today continues that trend, offering a particularly interesting take on low-resource fine-tuning — a topic that, as you can imagine, is especially compelling to me. Today's review is lazier than usual, I jotted down notes as I was read and then just had Opus clean them up afterward, followed by a few passes through Gemini, there's very little commentary on my end.

Post-training typically involves smaller datasets and narrower behavioral or knowledge domains compared to pre-training. Pre-training operates over trillions of tokens and hundreds of billions of parameters, so the network’s massive capacity is warranted. But in post-training, this scale becomes wasteful—why update terabits of weights to encode updates derived from gigabits of data? This intuition underpins parameter-efficient fine-tuning (PEFT). The populist form of PEFT is Low-Rank Adaptation, LoRA.

While it’s well-established that LoRA underperforms full fine-tuning (FullFT) in large-scale, pre-training-like regimes—where datasets exceed LoRA’s storage capacity—it’s less clear whether this gap persists for smaller datasets. Should LoRA really underperform when fine-tuning on modest data? And under what conditions can LoRA match FullFT in performance?

---

LoRA Refresher

Given a pretrained weight matrix $W \in \mathbb{R}^{d \times k}$, LoRA freezes $W$ and learns a low-rank update:

$$W' = W + \gamma BA,$$

where $B \in \mathbb{R}^{d \times r}$, $A \in \mathbb{R}^{r \times k}$, and $r \ll \min(d, k)$. LoRA thus encodes task-specific updates in a compact, low-dimensional subspace. During fine-tuning, $W$ is frozen (requires_grad=False), and only the smaller matrices $A$ and $B$ are trained.

Three key hyperparameters govern LoRA behavior:

Rank

The rank $r$ defines the intrinsic dimension of the adaptation subspace, bounding the rank of $\Delta W = BA$. The number of trainable parameters is:

$$\#\text{params}(\Delta W) = r(d + k),$$

scaling linearly with $r$ rather than $d$ or $k$. A small $r$ imposes a strong low-rank prior (heavier regularization, faster and cheaper), while a large $r$ allows more expressive updates, approaching FullFT as $r \to \min(d,k)$. In practice, ranks between 1–512 are common, balancing model size and dataset scale. Rank thus controls LoRA’s capacity relative to the dataset.

Alpha

Since $BA$ generally has smaller magnitude than $W$, the scaling factor $\gamma$ ensures comparable update strength. Libraries expose this as a scaling parameter $s = \alpha / r$, yielding:

$$W' = W + \tfrac{\alpha}{r} BA.$$

Increasing $\alpha$ amplifies update magnitude and gradient flow through $\Delta W$, effectively acting as a gain and modifying the effective learning rate. This decouples update magnitude from rank.

Target Modules

The target_modules setting specifies which weight matrices receive LoRA updates. In Transformer blocks, LoRA can be applied to:

• Attention: $W_Q, W_K, W_V, W_O$
• MLP: $W_{\text{in}}, W_{\text{out}}$ (also called gate/proj)

The choice of targets substantially impacts performance and efficiency.

---

Experimental Summary

The Thinking Machines Lab study systematically compares LoRA to FullFT across several settings: supervised instruction-tuning, reasoning tasks, and reinforcement learning. LoRA rank was varied over three orders of magnitude (1–512) and learning rates were swept broadly, selecting the pointwise minimum loss per step.

Using log loss (rather than sampling-based metrics) gave clean scaling relationships across training steps, dataset sizes, and ranks.

Rank and Loss Scaling

Training on Tulu-3 and subsets of OpenThoughts-3, FullFT and high-rank LoRAs show near-identical linear log-loss decay. Lower-rank LoRAs eventually flatten, reflecting insufficient capacity—once the adapter saturates, the model stops improving.

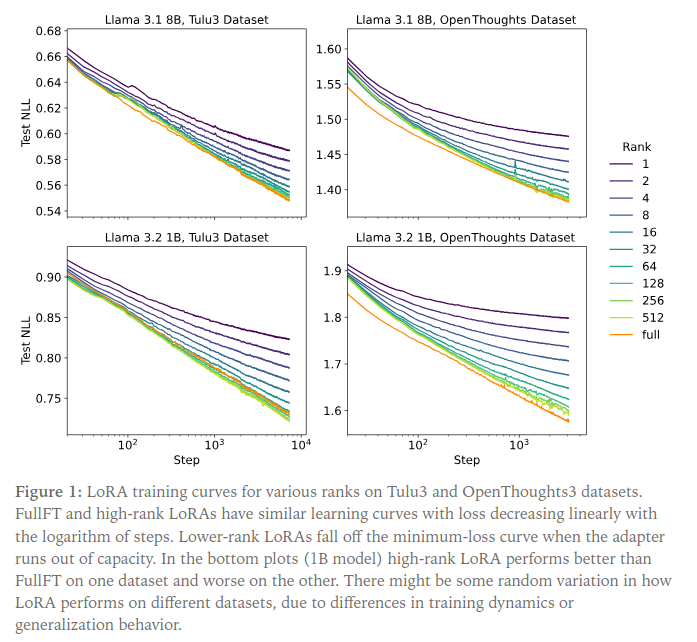
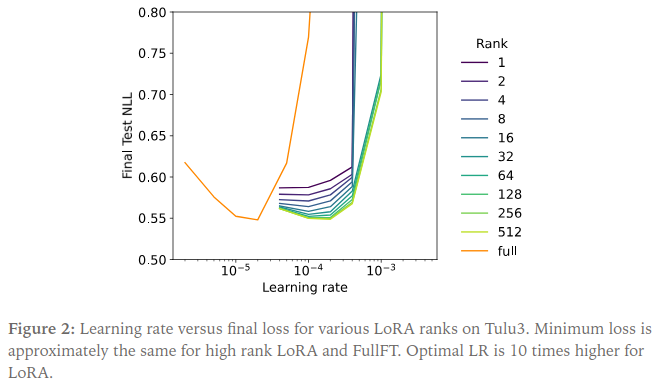
Interestingly, optimal learning rates vary little with rank: lower ranks favor slightly smaller LRs, but overall variation stays within a factor of two between ranks 4–512. FullFT, however, converges best at a learning rate roughly an order of magnitude lower than LoRA’s.

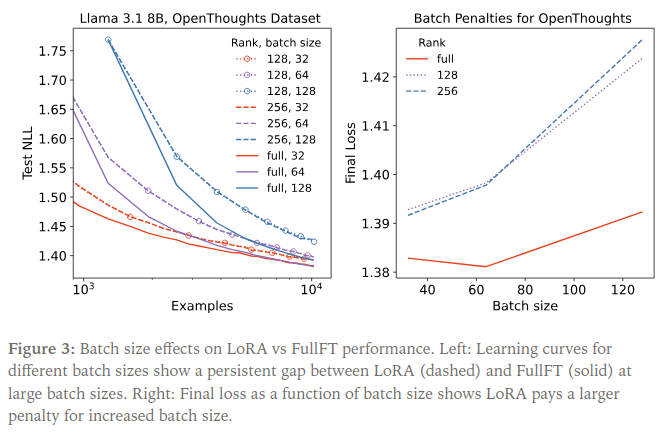
Batch Size Sensitivity

LoRA is less tolerant to large batch sizes than FullFT. As batch size increases, LoRA suffers a steeper performance penalty, independent of rank. This sensitivity appears intrinsic to LoRA’s product-of-matrices parameterization, not merely a consequence of limited capacity.

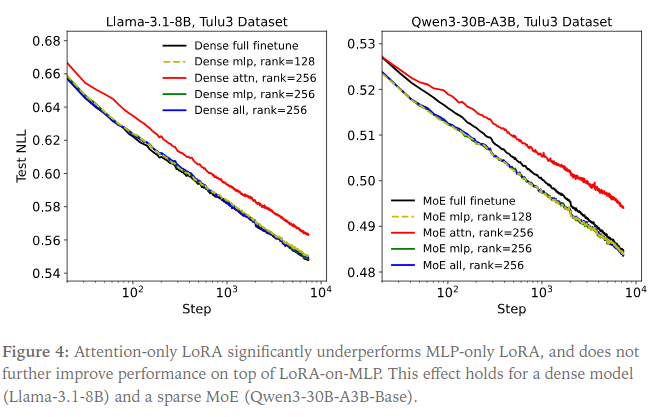
Target Module Selection

Practitioners often follow the original LoRA paper’s convention of applying adapters only to attention matrices ($W_Q, W_K, W_V, W_O$). However, LoRA Without Regret finds this suboptimal. Applying LoRA to MLP layers alone achieves the same minimum loss as full MLP+attention LoRA, while attention-only LoRA significantly underperforms. For MoE architectures, the authors train per-expert LoRA modules, scaling rank by the number of active experts to maintain a constant LoRA-to-FullFT parameter ratio.

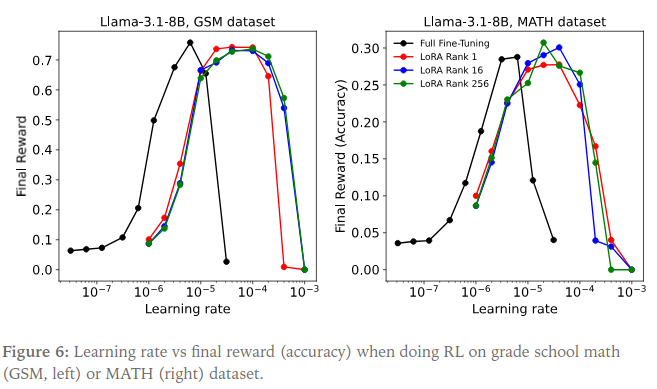
Reinforcement Learning

In reinforcement learning (RL), LoRA performs strikingly well—even at rank 1. Using a GRPO variant on MATH and GSM datasets, LoRA matched FullFT in both sample efficiency and peak performance.

The explanation is information-theoretic: supervised learning provides $O(\text{tokens})$ bits per episode, while policy gradients yield only $O(1)$ bits per episode (via the advantage signal). Thus, the effective information content of RL training is orders of magnitude smaller, easily captured by low-rank adapters. For example, in the MATH experiment (10k problems × 32 samples), only $\sim 320\text{k}$ bits of signal are available—far less than the 3M parameters in a rank-1 LoRA for Llama-3.1-8B. Similarly, DeepSeek-R1-Zero’s 5.3M episodes correspond to $<5.3\text{M}$ bits, again within LoRA’s representational capacity.

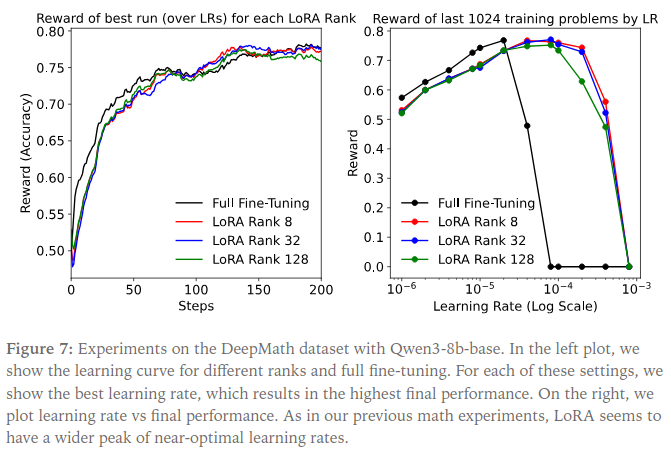
Follow-up experiments with Qwen3-8B-base on DeepMath confirmed the same trend: LoRA matches FullFT performance at ranks as low as 8, with a wider plateau of near-optimal learning rates.