how transformers think

having a mental model of what a transformer is and how it operates helps you quickly absorb new findings, providing an anchor to latch onto and integrate new learnings. a mental model isn't static; while some parts will be held with greater conviction - especially when solidified by repeated findings - the overall model must continuously shift and adapt. our understanding of neural networks is still nascent, so you need to be ready to challenge your own mental model. with that said, what follows in this post is mine.

we'll begin with a framework outlining the transformer as a whole. this is heavily inspired by early mechanistic interpretability work from anthropic. once this framework is established, we'll delve into the more opinionated components of my mental model.

i expect to come back to this post repeatedly as my model shifts, i'll probably make record of these changes somehow, don't know how yet.

A transformer framework

Within the context of this discourse, a transformer denotes an autoregressive, decoder-only transformer language model. Numerous variants and modifications to this foundational architecture exist, some exhibiting greater relevance than others; yet, the fundamental architectural constructs have demonstrated remarkable stability over time: a token embedding layer $\rightarrow$ a sequence of layers known henceforth as residual blocks $\rightarrow$ a token unembedding layer. Each residual block canonically comprises an attention mechanism succeeded by a multi-layer perceptron. The token embedding and unembedding layers are responsible for mapping a token—represented as a discrete integer identifier—to and from a $d$-dimensional floating-point vector representation.

The embedding matrix operates on an input sequence of $n$ tokens:

$\mathbf{t} = (t_1,t_2,\dots,t_n) \in V^{n}$

transforming it into an embedding matrix:

$H \in \mathbb{R}^{n \times d}$

where $H = [h_1, h_2, \dots, h_n]^T$ and each $h_i \in \mathbb{R}^{d}$ is the embedding for token $t_i$. However, for conceptual clarity, our analysis will concentrate on the embedding vector at the final sequence position, $h_n \in \mathbb{R}^{d}$, as this represents the next token prediction. Henceforth, the subscript $n$ on $h$ will be omitted for brevity, assuming we are referring to this final-position embedding, unless explicitly required for disambiguation. Consider the trajectory of this vector, $h \in \mathbb{R}^{d}$, as it propagates through the transformer's layers.

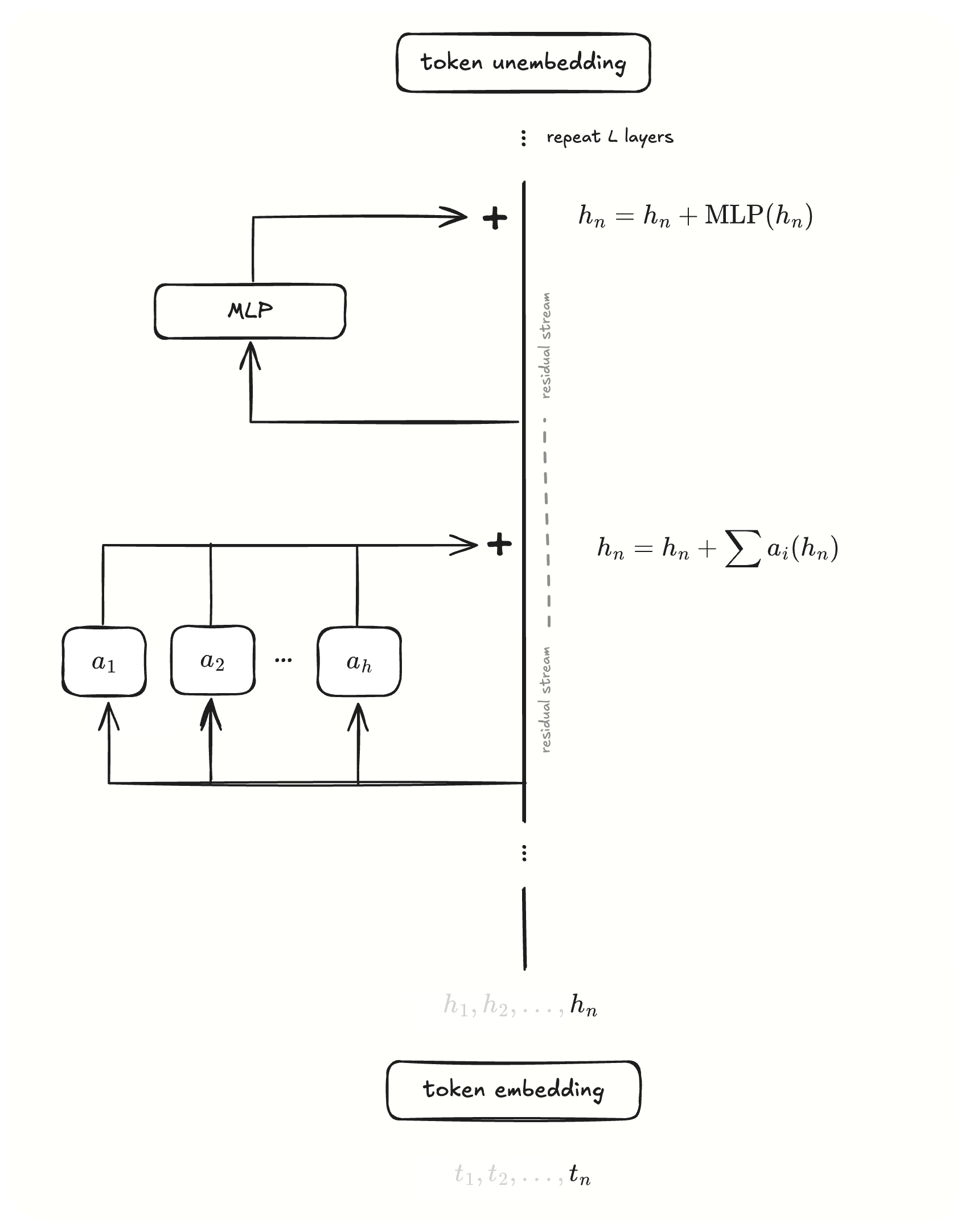
The most important concept to grasp here is the residual stream. For the present, defer a detailed examination of the internal operations within the attention and MLP layers. Instead, concentrate on the overarching information flow. Observe that each layer within this architecture interfaces with the residual stream by both reading from and writing to it. The residual stream, intrinsically, performs no computation; rather, it functions as a high-bandwidth communication bus facilitating inter-layer information exchange and state propagation. I find this to be one of the most insightful ways of thinking about the transformer. Each layer applies a learned linear transformation to project information from the incoming residual stream into its operational space (a "read" operation). Subsequent to its internal computations (e.g., attention or MLP), it employs another learned linear transformation to project its output, which is then additively merged back into the residual stream, forming the input for the subsequent layer (a "write" operation).

This linear, additive structure of the residual stream has some really cool and important consequences. Being a high-dimensional vector space (think of it as having lots of "lanes"), the residual stream allows distinct layers to communicate information selectively by encoding it within orthogonal or non-interfering subspaces. This means information can take an express route, effectively creating direct communication pathways across network depth. Once information is added to one of these subspaces, it tends to stick around through the following layers unless another layer specifically changes or removes it. Consequently, dimensions within the residual stream can be conceptualized as persistent memory slots, accumulating and refining information as it traverses the network.

A natural question arises: how is information propagated from prior token positions to this final position, which is critical for contextual understanding and next-token prediction? This necessitates an examination of the MLP and, more critically, the attention layers. While MLPs operate on each position independently, refining the representation at that position, attention layers, or more granularly, individual attention heads, serve the primary function of transposing and integrating information between different token positions.

Having established the residual stream as the primary conduit for information propagation, the natural question is: what actually happens inside these residual blocks? Specifically, what kind of processing are they doing with the information they've just read from the stream? Recall the two modules inside the residual block: Attention and MLP.

Attention facilitates inter-token communication, enabling the model to dynamically integrate information across different sequence positions. The mechanism operates by selectively aggregating information from the residual streams corresponding to a set of 'source' token positions and writing some processed version of that information to the residual stream of our "target" token. What's really neat is that how the model decides which tokens to get information from is pretty separate from what information it pulls out and how it changes that information before adding it to the target token's stream. Consequently, an attention head's operation can be effectively decomposed into two substantially independent computational sub-circuits:

The Query-Key (QK) circuit: This computes the attention pattern, typically a normalized score matrix $A \in \mathbb{R}^{n \times n}$ (for self-attention focusing on the final token's representation, we are interested in the $n$-th row, $A_{n,:}$, which dictates the contribution of each sequence position $j$ to the current position $n$). Essentially, it decides which other tokens' information is most important to pay attention to for the current token.

The Output-Value (OV) circuit: This circuit first projects the input token representations $h_j$ into 'value' vectors $v_j$ using a weight matrix $W_V$. It then combines these value vectors $v_j$ according to the attention pattern computed by the QK circuit. Finally, this aggregated information is projected using an output weight matrix $W_O$. Thus, the composite operation, effectively $W_O \left( \sum_{j} A_{n,j} (h_j W_V) \right)$, governs what information is extracted from the attended tokens and how it is transformed and integrated back into the residual stream at position $n$.

Note: The initial token embedding and final unembedding layers typically engage with only a subset of the $d$ dimensions of the residual stream. This leaves a significant portion of the dimensional capacity of the residual stream available for internal computations, feature learning, and information storage by the intermediate transformer blocks.

How do transformers think. Yes, they are thinking.

With this established common framework, we can now delve deeper. My model posits that transformers' capacity for complex reasoning, multilingual translation, and in-context learning suggests an internal "thought process" that transcends these mechanical operations. Transformers operate through distinct information processing regimes, fundamentally performing computation via precise geometric manipulations within their high-dimensional latent space. Their internal cognition is largely language-agnostic, with language-specific behaviors emerging primarily at the input and output interfaces. The transformer's mind, in essence, possesses a geometry of thought. Throughout I will use the notion of internal language as a springboard for this argument, partly because language is a well studied internal mechanisms that enables human interpretation.

a discrete-time dynamical system

Building upon the framework's description of the residual stream as a high-bandwidth communication bus, we can formalize its operation from a dynamical systems perspective. At its core, a decoder-only transformer maintains a high-dimensional latent state, $\mathbf{h}^{(\ell)} \in \mathbb{R}^d$, at each layer $\ell \in \{0, \dots, L\}$. Layer 0 represents the token embedding, and layer $L$ is the final hidden state before unembedding. The trajectory of the state vector $\mathbf{h} \in \mathbb{R}^d$ as it additively accumulates updates through the layers, $(\mathbf{h}^{(0)}, \mathbf{h}^{(1)}, \dots, \mathbf{h}^{(L)})$, defines the residual stream.

This progression can be precisely characterized as a discrete-time dynamical system, where each state $\mathbf{h}^{(\ell+1)}$ arises from the previous state $\mathbf{h}^{(\ell)}$ via the learned block update $f_{\text{block}}^{(\ell)}$:

$\mathbf{h}^{(\ell+1)} = \mathbf{h}^{(\ell)} + f_{\text{block}}^{(\ell)}(W_{\text{read}}^{(\ell)}\mathbf{h}^{(\ell)}).$

This formulation shows the residual stream effectively implementing an Euler integration of these learned increments. The profound implication of this additive, high-dimensional architecture is the emergence of cognitive compositionality: different computational modules can operate within almost-orthogonal subspaces of the stream, contributing their results without destructive interference.

the dual space hypothesis

A fundamental insight into transformer cognition is the decomposition of any latent state vector $\mathbf{h}$ in the residual stream into two orthogonal components:

$\mathbf{h} = \mathbf{h}_T + \mathbf{h}_{T^{\perp}}$

1. The Token Subspace ($T$): This subspace is spanned by the rows of the unembedding matrix $U$. It can be visualized as a "thin ellipsoid" within the larger latent space. The token subspace $T$ is directly involved in logit production ($z = U\mathbf{h}_T = U(\text{proj}_T \mathbf{h})$). Information that fails to project onto $T$ is invisible to the softmax output layer.

2. The Orthogonal Concept Space ($T^{\perp}$): This is the complementary, typically much larger, $(d - \dim T)$-dimensional workspace. It is here, in this "hidden room," that the majority of the transformer's actual computation and conceptual manipulation occurs. Empirically, the token energy, $\|\mathbf{h}_T\|^2 / \|\mathbf{h}\|^2$, remains small for a significant portion of the network's depth (often up to half), indicating that the early and middle layers primarily operate within this conceptual substrate $T^{\perp}$.

the three phase trajectory of thought

Transformer computation universally follows a three-phase processing model, reflecting a coarse chronology as information traverses the layers:

1. Phase 1: De-tokenization and Concept Formation (Early Layers) The initial layers are tasked with mapping the arbitrary, discrete structure of input tokens into rich, distributed semantic representations. During this phase, the latent representations exhibit minimal projection onto the token subspace, meaning $\|\mathbf{h}_T\|^2 \ll \|\mathbf{h}_{T^{\perp}}\|^2$. Neurons in these layers often respond to multi-token words or abstract concepts, actively working to transcend tokenization boundaries and construct a language-agnostic conceptual representation.

2. Phase 2: Conceptual Simulation and Manipulation (Middle Layers) This is where the bulk of the transformer's depth is concentrated and where its core "reasoning" capabilities are enacted. The model manipulates abstract representations, performs logical operations, tracks states, and maintains a distributed representation of semantic context. These operations occur predominantly in $T^{\perp}$, which explains why middle-layer activations can appear chaotic or inscrutable when viewed solely through the "logit lens" (i.e., projections onto $T$). This phase is the true locus of simulation and is almost invisible to logit-based probing techniques. The conceptual information processed here is largely language-agnostic, operating in what can be termed a computational interlingua—a distributed representational system optimized for the model's internal processing rather than any specific human language. This is where multilingual features emerge, representing shared conceptual pathways activated regardless of input language (e.g., the concept of "antonymy").

3. Phase 3: Re-tokenization (Final Layers) In the final layers, the transformer must convert its abstract conceptual representations back into concrete tokens for output. Here, language-specific processing becomes dominant. The token energy spikes dramatically, such that $\|\mathbf{h}_T\|^2 \approx \|\mathbf{h}\|^2$, as the model projects its conceptual state onto the token subspace $T$. Specialized neurons mediate this conversion from abstract concepts to specific vocabulary items, a process highly dependent on the target language.

the cognition within $T^{\perp}$

Several key mechanisms enable the complex computations within the conceptual substrate $T^{\perp}$:

• Attention as State-Coupled Teleportation: Inside each block, the attention mechanism is pivotal. It decomposes into a routing circuit, $A = \text{softmax}(QK^\top/\sqrt{d_k})$, and a payload circuit $V \to OV$. The routing circuit is a critical reason for transformers' scaling success. Because $A$ depends bilinearly on $\langle \mathbf{q}_i, \mathbf{k}_j \rangle$, the optimizer can create near-binary attention patterns—effectively discrete pointers—while keeping all operations differentiable. A single attention head can thus "teleport" an entire low-rank slice of another token's residual state (from a previous position in the sequence) into the current processing position. The subsequent payload MLP can then non-linearly remix this information. In effect, the network dynamically builds skip connections through time, granting it the ability to simulate arbitrarily non-Markovian state machines within a strictly causal architecture.

• Episodic State Simulation: Transformers can be understood as performing state simulation. Rather than linearly updating a single "global context vector" from left to right, each prediction step $n \mapsto n+1$ is better viewed as an independent episode. For each step, the model constructs, from scratch, a latent micro-world within $T^{\perp}$ that is conditionally sufficient to determine the next-token distribution $p_{\theta}(x_{n+1}|x_{\le n})$. The training objective, $\theta^\star = \text{arg min}_{\theta} \mathbb{E}_{x_{1:N}} \sum_{n=1}^{N} -\log p_{\theta}(x_{n+1}|x_{\le n})$, only requires that the final layer state $\mathbf{h}^{(L)}$ deterministically encodes this conditional distribution. This means the network is not compelled to "remember" its previous micro-world in a fixed way; it is free to jettison or reinterpret any earlier claim if subsequent text provides contradictory or overriding information. This freedom manifests as state branching: mutually inconsistent futures or interpretations can coexist in superposition within $T^{\perp}$ until the attention mechanism, guided by disambiguating evidence in the context, effectively "collapses the branch." This explains the remarkable ability to handle non-linear context dependencies, such as when new information invalidates earlier statements.

• The Geometry of Thought The orthogonal concept space $T^{\perp}$ possesses a rich geometric structure reflecting semantic relationships. This space is organized around abstract conceptual primitives rather than language-specific lexical items. For instance, in multilingual settings, concepts like "antonymy" or "size" are represented by shared features or regions in $T^{\perp}$, activated regardless of the specific input language. What changes for different languages is primarily the language identification information that routes the final output to the appropriate lexicon during re-tokenization. These functional clusters implement specific semantic operations and form the basis of the computational interlingua. The geometric relationships between these conceptual clusters are preserved across languages, explaining cross-lingual transfer effects.

next distribution prediction

A critical, often overlooked, aspect is that transformers do not simply predict "the most likely next token." They are optimized to model entire probability distributions over all possible continuations. The cross-entropy loss

$\mathcal{L} = -\sum_{t \in V} p_{\text{true}}(t) \log p_{\text{model}}(t)$

rewards the network for accurately emitting the entire distribution. Consequently, the internal representations must encode a measure over continuation worlds. This probabilistic thinking is essential for maintaining appropriate degrees of uncertainty and for representing multiple possible world states simultaneously.

When the true underlying distribution is sharply peaked (e.g., in predicting the next token in a piece of code), these factors may align early with a single token vector, leading to an "early collapse" pattern observable via the logit lens. Conversely, when the distribution is broad (e.g., in creative prose), the factors can remain abstract until the final few layers, where multiple token vectors are softly superposed. This distributional perspective underpins the transformer's abilities in in-context learning and generalization, allowing adaptation to novel patterns without explicit parameter updates. Crucially, this adaptability stems from the transformer's stateless autoregressive process: the generation of each token is grounded by a re-evaluation of the complete discrete symbolic history. This constant re-grounding enables the self-attention mechanism to dynamically shape the internal measure over continuation worlds from the input prefix, effectively reconfiguring latent factors to condition the output distribution. Such contextual modulation of the predictive measure—achieved without the continuity biases inherent in explicitly stateful recurrent models—allows a single pretrained transformer to exhibit highly adaptive, specialized behaviors based on few-shot prompting. The resulting richness of this context-dependent learned measure also provides a robust basis for diverse sampling strategies (e.g., nucleus sampling, temperature scaling) that modulate the output distribution to control generative stochasticity and creativity.

"but models are thinking in english!!"

A recurring observation in multilingual transformers is an apparent privileging of English. This model posits that the "English bias" is primarily a surface phenomenon of the token subspace $T$ and a geometric artifact, rather than evidence of conceptual processing occurring "in English." Due to imbalances in training data, English token vectors tend to tile the token subspace $T$ more densely than those of other languages. This creates a geometric bias where English tokens become more accessible as "lexical anchors." When conceptual information from $T^{\perp}$ needs to be projected onto $T$ (either for intermediate routing or for generating final logits), English tokens are statistically more likely to receive probability mass simply because they are geometrically "closer" to more regions of the concept space. This explains the characteristic "pivot shape" observed in latent trajectories during tasks like French-to-Chinese translation. The norm of the English token projection, $\|\mathbf{h}_T^{\text{EN}}\|$, might rise around the middle layers before the target Chinese component, $\|\mathbf{h}_T^{\text{ZH}}\|$, dominates in the final layers. The conceptual path can be visualized as: $\mathbf{h}^{(\ell)} \xrightarrow[\text{pivot}]{\ell\simeq 0.6L} (\mathbf{h}_{T^{\perp}}, \mathbf{h}_T^{\text{EN}}) \xrightarrow[\text{retokenise}]{\ell\simeq 0.9L} (\mathbf{h}_{T^{\perp}}, \mathbf{h}_T^{\text{ZH}})$ Crucially, the component in the conceptual space, $\mathbf{h}_{T^{\perp}}$, which carries the core semantic content, barely flinches during this pivot. Only its lexical "shadow" in $T$ slides from an English projection to a Chinese one. This pivot is therefore largely a decoding artifact or a consequence of token-space geometry and training priors, not an indication of epistemic dependence on an English ontology or that the model genuinely "thinks in English." The bulk of its cognition remains language-agnostic within $T^{\perp}$.

depth depth depth

The significant depth of modern transformers is a computational necessity dictated by the three-phase processing model:

1. De-tokenization requires multiple layers to effectively overcome arbitrary tokenization boundaries and construct coherent, distributed semantic representations from discrete inputs.
2. Conceptual manipulation and simulation involve complex, multi-step reasoning and iterative refinement of abstract representations. This core phase benefits most from increased depth, allowing for the gradual transformation of representations from input-oriented to output-oriented.
3. Re-tokenization must map abstract concepts back to specific vocabulary tokens, often involving multiple steps to narrow down from broad semantic fields to precise lexical choices in the target language. Shallow transformers struggle with complex reasoning tasks precisely because they lack the necessary depth to fully develop and manipulate the abstract conceptual representations required for sophisticated computation in the orthogonal concept space $T^{\perp}$.

to conclude

The transformer, as I conceptualize it, is an engine for abstract conceptual manipulation. It builds complex thoughts in a space largely hidden from direct token-level scrutiny ($\mathbf{h}_{T^{\perp}}$). Its "native tongue" is this abstract feature space. The observed English-centricity is a consequence of its upbringing and the resulting structure of its token output interface ($T$), making English a sort of "first port of call" for projections of thought, rather than the inherent language of its internal reasoning. The true "thought" is more universal, more abstract, and only dons specific linguistic clothes at the very end of its intricate journey through the network's layers.