multi-head latent attention

DeepSeek V3 is an astonashing feat of engineering, model performance aside (the topic seems contentious, i've heard mixed opinions so far, apparently it keeps getting stuck in a reasoning spiral), being able to train a model of this capacity on a 2048 H800 cluster.... in just 4 GPU days? Crazy. They only spent $5M dollars training this thing. Also, from what I hear, the DeepSeek team is barely >100 people, and it's all in-house Chinese talent. I mean if you were worried about China's development before... yeah I don't know, they're fucking good that's all I know.

enough raving about the DeepSeek team, one of my favorite things about DeepSeek's models, are their attention mechanism, so i'd like to provide a formal introduction to: Multi-head Latent Attention; MLA. MLA was first introduced in DeepSeek V2, back in spring earlier this year i believe? I spent some time digging into it back then, but unfortunately my mind is slipping on the details so i'm going to take another pass at it and you can come along with me. i'll be looking at it through a the perspective of the historical evolution of attention mechanisms: MHA -> MQA -> GQA -> MLA. The content below is heavily inspired (a considerable amount os directly translated) by a post from Jianlin Su, the author of RoPE, who runs an incredible blog, in chinese.

MHA

Multi-head attention is the traditional attention mechanism defined in Attention is all you need. Suppose the input sequence consists of row vectors $x_1, x_2,...,x_l$ where $x_i \in \mathbb{R}^{d}$, then MHA is formally represented as:

$$\begin{aligned} \mathbf{o}_t &= [\mathbf{o}_t^{(1)}, \mathbf{o}_t^{(2)}, \dots, \mathbf{o}_t^{(h)}] \\ \mathbf{o}_t^{(s)} &= \text{Attention}(\mathbf{q}_t^{(s)}, \mathbf{k}_{\leq t}^{(s)}, \mathbf{v}_{\leq t}^{(s)}) \triangleq \frac{\sum_{i \leq t} \exp(\mathbf{q}_t^{(s)} \cdot \mathbf{k}_i^{(s)\top}) \mathbf{v}_i^{(s)}}{\sum_{i \leq t} \exp(\mathbf{q}_t^{(s)} \cdot \mathbf{k}_i^{(s)\top})} \\ \mathbf{q}_i^{(s)} &= \mathbf{x}_i \mathbf{W}_q^{(s)} \in \mathbb{R}^{d_k}, \quad \mathbf{W}_q^{(s)} \in \mathbb{R}^{d \times d_k} \\ \mathbf{k}_i^{(s)} &= \mathbf{x}_i \mathbf{W}_k^{(s)} \in \mathbb{R}^{d_k}, \quad \mathbf{W}_k^{(s)} \in \mathbb{R}^{d \times d_k} \\ \mathbf{v}_i^{(s)} &= \mathbf{x}_i \mathbf{W}_v^{(s)} \in \mathbb{R}^{d_v}, \quad \mathbf{W}_v^{(s)} \in \mathbb{R}^{d \times d_v} \end{aligned}$$

An example configuration (Llama 3.1 70B) of the above parameters is $d = 8192, d_k = 128, h=64$. Note that $d_k = d / h$ is common practice.

During inference a causal autoregressive language model generates tokens recursively, meaning the generation of token $t + 1$ does not affect the previously computed matrices $\mathbf{k}_{≤t}^{(s)}, \mathbf{v}_{≤t}^{(s)}$. These matrices can be cached in a KV cache to reduce redundant computation, trading compute for memory. However the KV cache grows with both the model size and input length. At sufficiently long context lengths, the KV cache can consume the majority of GPU memory, often surpassing the memory required for model parameters and activations (albeit flash attention and other low level optimizations have aleviated the issue). This scaling issue makes it a bottleneck for efficient inference, especially for models serving long inputs.

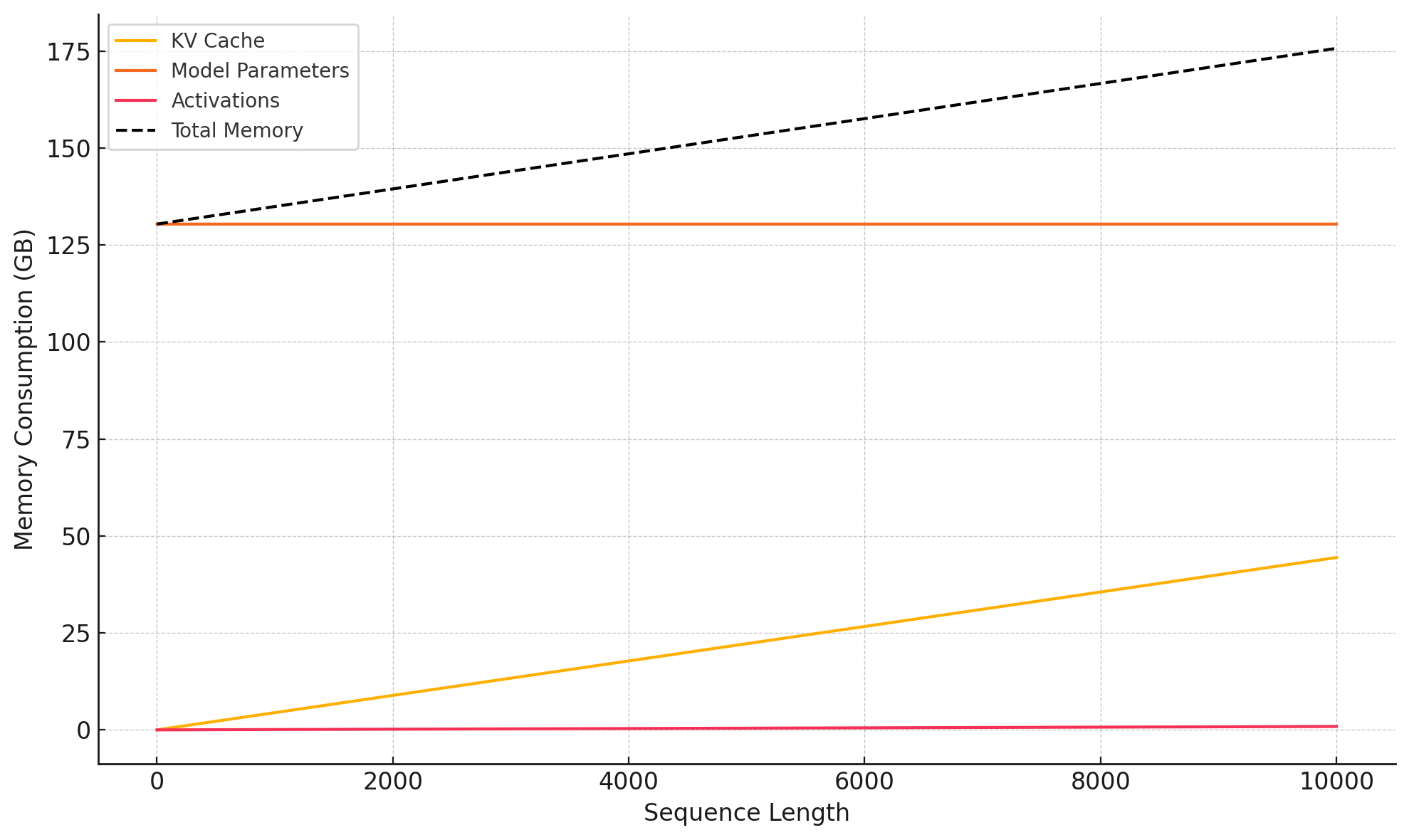
A solution would be to deploy such models across multiple cards, or when necessary across multiple machines. However, a guiding principle when deploying models across a GPU cluster is that intra-card communication bandwidth > inter-card communication bandwidth > inter-machine communication bandwidth. The more devices a deployment spans, the higher the communication overhead + cost becomes. Thus, we aim to minimize the KV cache such that we can serve long context models on as few GPUs as possible, with the ultimate goal of lowering inference costs.

This provides the guiding motivation behind the subsequent developments to the attention mechanism.

MQA

Multi-query attention (MQA) is the extreme alternative to MHA, published in the 2019 paper Fast Transformer Decoding: One Write-Head is All You Need it represents the cautionary reaction to the apparent problems of the KV Cache. If one understands MHA, understanding MQA is simple: let all attention heads share the same key and values. Formally, this means canceling the superscripts of all $k, v$ in MHA:

$$\begin{aligned} \mathbf{o}_t &= [\mathbf{o}_t^{(1)}, \mathbf{o}_t^{(2)}, \dots, \mathbf{o}_t^{(h)}] \\ \mathbf{o}_t^{(s)} &= \text{Attention}(\mathbf{q}_t^{(s)}, \mathbf{k}_{\leq t}^{\cancel{(s)}}, \mathbf{v}_{\leq t}^{\cancel{(s)}}) \triangleq \frac{\sum_{i \leq t} \exp(\mathbf{q}_t^{(s)} \mathbf{k}_i^{\cancel{(s)}\top}) \mathbf{v}_i^{\cancel{(s)}}}{\sum_{i \leq t} \exp(\mathbf{q}_t^{(s)} \mathbf{k}_i^{\cancel{(s)}\top})} \\ \mathbf{q}_t^{(s)} &= \mathbf{x}_t \mathbf{W}_q^{(s)} \in \mathbb{R}^{d_k}, \quad \mathbf{W}_q^{(s)} \in \mathbb{R}^{d \times d_k} \\ \mathbf{k}_i^{\cancel{(s)}} &= \mathbf{x}_i \mathbf{W}_k^{\cancel{(s)}} \in \mathbb{R}^{d_k}, \quad \mathbf{W}_k^{\cancel{(s)}} \in \mathbb{R}^{d \times d_k} \\ \mathbf{v}_i^{\cancel{(s)}} &= \mathbf{x}_i \mathbf{W}_v^{\cancel{(s)}} \in \mathbb{R}^{d_v}, \quad \mathbf{W}_v^{\cancel{(s)}} \in \mathbb{R}^{d \times d_v} \end{aligned}$$

In practice, the $k, v$ heads are broadcast in-place across $q$ heads during computation. This reduces the KV Cache to $1 / h$ of the original size, which is a significant reduction. It does however suffer in performance, but MQA supports claim this can be offset by increased training time. The "saved" parameters can be shifted to the FFN to make up for some of the lost performance.

GQA

Grouped Query Attention is the generalized version of MHA and MQA, published in the 2022 paper GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints. GQA divides the KV heads into $g$ groups (where $g$ evenly divides $h$), where each group is paired with 1 or more query heads. Formally, this is expressed as:

$$\begin{aligned} \mathbf{o}_t &= [\mathbf{o}_t^{(1)}, \mathbf{o}_t^{(2)}, \dots, \mathbf{o}_t^{(h)}] \\ \mathbf{o}_t^{(s)} &= \text{Attention}\left(\mathbf{q}_t^{(s)}, \mathbf{k}_{\leq t}^{\left(\lceil sg/h \rceil\right)}, \mathbf{v}_{\leq t}^{\left(\lceil sg/h \rceil\right)}\right) \triangleq \frac{\sum_{i \leq t} \exp\left(\mathbf{q}_t^{(s)} \mathbf{k}_i^{\left(\lceil sg/h \rceil\right)\top}\right) \mathbf{v}_i^{\left(\lceil sg/h \rceil\right)}}{\sum_{i \leq t} \exp\left(\mathbf{q}_t^{(s)} \mathbf{k}_i^{\left(\lceil sg/h \rceil\right)\top}\right)} \\ \mathbf{q}_t^{(s)} &= \mathbf{x}_t \mathbf{W}_q^{(s)} \in \mathbb{R}^{d_k}, \quad \mathbf{W}_q^{(s)} \in \mathbb{R}^{d \times d_k} \\ \mathbf{k}_i^{\left(\lceil sg/h \rceil\right)} &= \mathbf{x}_i \mathbf{W}_k^{\left(\lceil sg/h \rceil\right)} \in \mathbb{R}^{d_k}, \quad \mathbf{W}_k^{\left(\lceil sg/h \rceil\right)} \in \mathbb{R}^{d \times d_k} \\ \mathbf{v}_i^{\left(\lceil sg/h \rceil\right)} &= \mathbf{x}_i \mathbf{W}_v^{\left(\lceil sg/h \rceil\right)} \in \mathbb{R}^{d_v}, \quad \mathbf{W}_v^{\left(\lceil sg/h \rceil\right)} \in \mathbb{R}^{d \times d_v} \end{aligned}$$

GQA generalizes MHA and MQA by varying the number of attention groups $g$. When $g = h$ it replicates MHA; when $g = 1$ it corresponds to MQA; and for $1 < g < h$, it compresses the KV cache by a factor of $g / h$. This flexibility makes GQA a more versatile and efficient implementation, as it allows precise control over the trade-off between compression and computational cost.

An important advantage of GQA is its inherent support for parallelism in attention computation. In large models, where a single GPU is insufficient to store the full model, attention computations can be parallelized across heads, which are independently processed before concatenation (see formulas above). By selecting $g$ to align with the number of GPUs used for parallelization, GQA minimizes inter-device communication overhead, enhancing scalability and efficiency.

MLA

Now that we've laid the groundwork with MHA, MQA, and GQA, we're ready to tackle Multi-head Latent Attention (MLA). At first glance, MLA introduces a low-rank projection of the KV Cache, to which a reader may question "Why did it take so long until someone proposed a low rank decomposition of the KV Cache considering how long LoRA has been around?"

However, consider what happens in GQA when we stack all $K, V$ together:

$$\begin{aligned} \underbrace{\left[\mathbf{k}_i^{(1)}, \dots, \mathbf{k}_i^{(g)}, \mathbf{v}_i^{(1)}, \dots, \mathbf{v}_i^{(g)}\right]}_{\mathbf{c}_i \in \mathbb{R}^{g(d_k + d_v)}} &= \mathbf{x}_i \underbrace{\left[\mathbf{W}_k^{(1)}, \dots, \mathbf{W}_k^{(g)}, \mathbf{W}_v^{(1)}, \dots, \mathbf{W}_v^{(g)}\right]}_{\mathbf{W}_c \in \mathbb{R}^{d \times g(d_k + d_v)}} \end{aligned}$$

If we consider $c_i$ to represent the concatenated $k, v$, and the corresponding projection matrices as $W_c$ we see that GQA is already performing a low-rank projection. Generally, we have that $d_c = g(d_k + d_v) < d$, so the transformation from $x_i$ to $c_i$ is a low-rank projection. As such, the contribution of MLA is not the low rank projection itself, but rather what happens after the projection.

Part 1

GQA downprojects the $x_i$ into $2 \times h \times g$, splits the matrice into two halves for $K$ and $V$, then further divides this into $g$ parts and replicates each part $h \ g$ times to "make up" the $K$ and $V$ required for the $h$ heads. While effective, this approach imposes structural rigidity, enforcing a fixed grouping and replication scheme. MLA recognizes that these operations are simple linear transformations, and therefor replaces them with a learned learned linear transformation. This transformation projects $x_i$ into a shared latent space, capturing features in a compressed form and increasing model capacity.

$$c_i = x_i W_c \in \mathbb{R}^{d_c}, \quad W_c \in \mathbb{R}^{d \times d_c}.$$

Once $c_i$ is derived, it serves as the basis for generating head-specific keys and values. For each attention head $s$, a linear transformation is applied to map $c_i$ into the full query space $\mathbb{R}^{d_k}$:

$$k_i^{(s)} = c_i W_k^{(s)} \in \mathbb{R}^{d_k}, \quad W_k^{(s)} \in \mathbb{R}^{d_c \times d_k}$$ $$v_i^{(s)} = c_i W_v^{(s)} \in \mathbb{R}^{d_v}, \quad W_v^{(s)} \in \mathbb{R}^{d_c \times d_v}.$$

Theoretically, this increases model capacity, but the goal of GQA is to reduce KV Cache, so what happens to our cache? In GQA, we would cache our downprojected $k_i, v_i$, however, MLA's approach recreates all $h$ KV heads, causing the KV Cache size to revert to that of MHA? Interestingly, the authors leave this be during training, but then circumvent this issue during inference by caching only $c_i$ and fusing the projection matrices $W_k, W_v$ with subsequent operations. Notably, $c_i$ is independent of $s$, meaning that it is shared across all heads, MLA transforms into MQA during inference.

Part 2

Everything seems exemplary at first glance; but the observant eye will that our inference scheme is incompatible with RoPE. Earlier, we mentioned that we can cache $c_i$ during inference, not needing to compute $k_i$, why was that? In the dot product attention, $q$ and $k$ are combined as

$$\begin{aligned} \mathbf{q}_t^{(s)} \mathbf{k}_i^{(s)\top} &= \left(\mathbf{x}_t \mathbf{W}_q^{(s)}\right) \left(\mathbf{c}_i \mathbf{W}_k^{(s)}\right)^\top = \mathbf{x}_t \left(\mathbf{W}_q^{(s)} \mathbf{W}_k^{(s)\top}\right) \mathbf{c}_i^\top \end{aligned}$$

with the last reformulation, we can combine $\mathbf{W}_q^{(s)} \mathbf{W}_k^{(s)\top}$ as the projection matrix for Q, replacing $k_i$ with $c_i$. Now, this was possible because $\mathbf{W}_q^{(s)} \mathbf{W}_k^{(s)\top}$ are simple linear transformations with no external dependencies. However, RoPE changes the dot product attention of MLA:

$$\begin{aligned} \mathbf{q}_t^{(s)} &= \mathbf{x}_t \mathbf{W}_q^{(s)} \mathbf{R}_t, \quad \mathbf{k}_i^{(s)} = \mathbf{c}_i \mathbf{W}_k^{(s)} \mathbf{R}_i \\ \mathbf{q}_t^{(s)} \mathbf{k}_i^{(s)\top} &= \mathbf{x}_t \Big(\mathbf{W}_q^{(s)} \mathbf{R}_t \mathbf{R}_i^\top \mathbf{W}_k^{(s)\top}\Big) \mathbf{c}_i^\top = \mathbf{x}_t \Big(\mathbf{W}_q^{(s)} \mathbf{R}_{t-i} \mathbf{W}_k^{(s)\top}\Big) \mathbf{c}_i^\top \end{aligned}$$

which introduces a term that depends on the position difference $t - i$. $R_{t-i}$ encodes dynamic relative position information, at runtime, breaking the assumption of position independence that MLA relies on to cache only $c_i$. One might be asking why we can't just cache the compressed representation $c_i$ and recompute $k_i$ on demand, this would still reduce the memory footprint of our KV Cache? Well we'd have to re-calculate $k_i$ at every token position, effectively making the cache redundant. Unfortunately, this problem is fundamental to RoPE, and even though DeepSeek reached out to Jianlin himself they were unable to find a clean solution.

The published approach is a hybrid design. It splits the representation of queries $q_t^{(s)}$ and keys $k_i^{(s)}$ into two distinct components: content dimensions $d_k$ and RoPE dimensions $d_r$. These two components serve different roles while preserving the benefits of both MLA's KV cache reduction and RoPE's relative position encoding.

For queries:

$$q_t^{(s)} = [x_t W_{qc}^{(s)}, x_t W_{qr}^{(s)} R_t],$$

and for keys:

$$k_i^{(s)} = [c_i W_{kc}^{(s)}, x_i W_{kr}^{(s)} R_i].$$

The content dimensions $d_k$ are derived from the shared latent representation $c_i = x_i W_c \in \mathbb{R}^{d_c}$, which is cached across all heads and independent of position. These dimensions can continue as described in part 1 above.

The RoPE dimensions $d_r$ are derived directly from the input $x_i$ and are position-dependent through the application of $R_i$. These dimensions capture positional information and interact during the attention computation to retain RoPE's property:

$$R_t R_i^\top = R_{t-i}.$$

This ensures that relative positional relationships are encoded, preserving the benefits of RoPE without needing to embed positional encoding into $c_i$.

During attention computation, the score for the query at position $t$ and key at position $i$ becomes:

$$q_t^{(s)} k_i^{(s)\top} = \big(x_t W_{qc}^{(s)}\big) \big(c_i W_{kc}^{(s)}\big)^\top + \big(x_t W_{qr}^{(s)} R_t\big) \big(x_i W_{kr}^{(s)} R_i\big)^\top$$

Here, the content dot product $\big(x_t W_{qc}^{(s)}\big) \big(c_i W_{kc}^{(s)}\big)^\top$ relies only on $c_i$, allowing the earlier "dot product trick" (fusing $W_q^{(s)}$ and $W_k^{(s)}$) to be retained. Meanwhile, the RoPE dot product $\big(x_t W_{qr}^{(s)} R_t\big) \big(x_i W_{kr}^{(s)} R_i\big)^\top$ directly incorporates relative positional information using $R_t R_i^\top = R_{t-i}$.

Only a small additional overhead for $d_r$ (e.g., $d_r = d_k / 2$) is added to the KV cache for shared RoPE dimensions, minimizing memory growth.

concluding thoughts

pff, okay that was a mouthful. MLA is honestly quite difficult to just grok upon first look imo, if it weren't for the RoPE embeddings it would probably be a lot easier honestly, apparently they did try alternative embeddings schemes but nothing worked as well as RoPE. The whole solution would be a lot cleaner as well, but alas... Either way this blog post as a whole by Jianlin is fantastic, I have yet to find a better deep dive on MLA. Heavily enjoyed this, thank you Jianlin.