Visual Autoregressive Modeling: Scalable Image Generation via Next-Scale Prediction

i don't typically cover the cv domain but this paper won 'best paper' at neurips and i heard its a really good paper for people unfamiliar with the field. you may also have heard of the controversy surrounding this paper, the paper is a collaboration between peking university and bytedance, and bytedance is suing the main author because apparently he was sabotaging other projects, slowing down colleagues, everything in attempt to hog more compute for his project. this project. which now won best paper and outperformed previous autoregressive image modelling sota's by 10x. crazy story. anyway let's get into it.

in image generation, diffusion models are unmatched in their performance, they've been the staple architecture with adopters such as StableDiffusion and SORA. meanwhile, despite the undeniable success of autoregressive (ar) models in the language domain, their performance in computer vision has stagnated, falling far behind diffusion models. but why? in language, ar models have been celebrated for their scalability and generalizability. so why hasn’t this translated to the image domain? just like text, humans have curated an immense amount of visual data available online. we have the data, much like we do for llms, yet performance hasn't reflected this. so what’s different?

well, it's simple really. text has a natural causal order, images don't. traditional autoregressive approaches attempt to turn images into a next-image-token prediction task, forcing them into a structure originally designed for language.

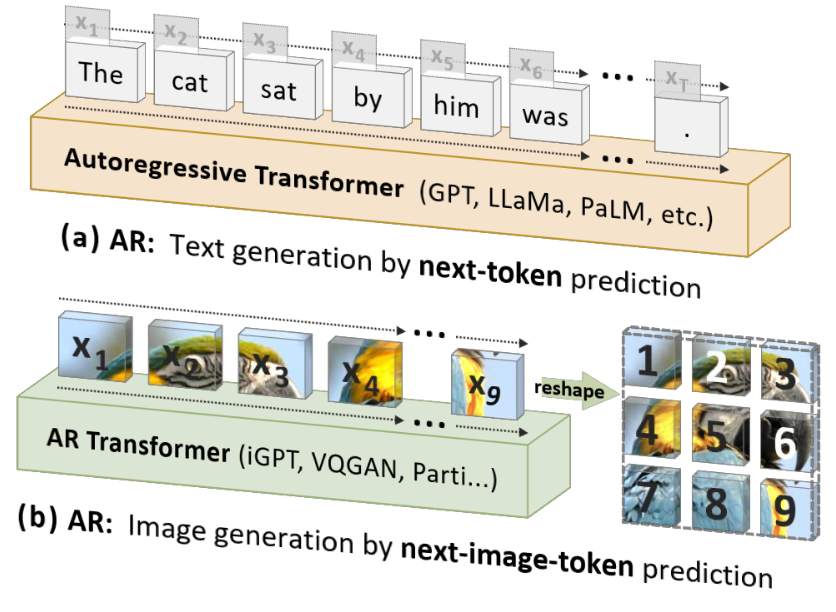
in this approach, images are patchified, discretized into tokens, and arranged into a 1d sequence—typically following a raster-scan order (left-to-right, top-down). this introduces an inductive prior originally designed for text. for text, this makes sense because it inherently follows a 1d order. for images, however, this assumption is unnatural. to address this mismatch, researchers often rely on positional embeddings (like rope embeddings) to encode spatial relationships into the neural network. despite these efforts, this workaround has yet to achieve significant success. whether the raster-scan order itself is the main limitation remains debatable, but the results of this paper suggest it might be. that’s because this paper, var, directly tackles the shortcomings of raster-scan ordering.

autoregressive modeling inherently requires defining an order for the data. var redefines what order means for images by shifting the objective from predicting the next image token to predicting the next resolution (or scale). instead of processing images token by token, the model generates entire images autoregressively from coarse to fine scales. humans naturally perceive images hierarchically, which suggests that a multi-scale, coarse-to-fine ordering offers a much better inductive prior. this idea, rooted in studies of human vision, mirrors how CNNs process images—aggregating information progressively through receptive fields. CNNs are known to capture different levels of detail across their layers, making this coarse-to-fine approach both intuitive and effective.

there are two stages to training a VAR model, the first is to train a multi-scale VQ autoencoder that transforms an image into $K$ token maps $R = (r_1, r_2, ..., r_K)$, the second is to train a transformer on $R = ([s], r_1, r_2, ..., r_{K-1})$ predicting $R = (r_1, r_2, ..., r_K)$. i won’t go into details about the VAR transformer itself—it’s a standard gpt-2-style transformer and likely nothing you haven’t seen before. what's interesting here is $r_k$, and to understand $r_k$ we'll take a look at the tokenizer, the multi-scale VQVAE.

vqvae. before understanding a multi-scale VQVAE, which to be clear is a novel architecture introduced in this paper, one needs to understand a vanilla VQVAE. i'll run through this briefly, click here if you want a more thorough explanation. VQVAE's are used in autoregressive image modelling to tokenize a image into discrete tokens. like the name suggests, the architecture is of classical autoencoder style, but the latent space representation, or embedding space, comes from a discrete vocabulary, known as a codebook.

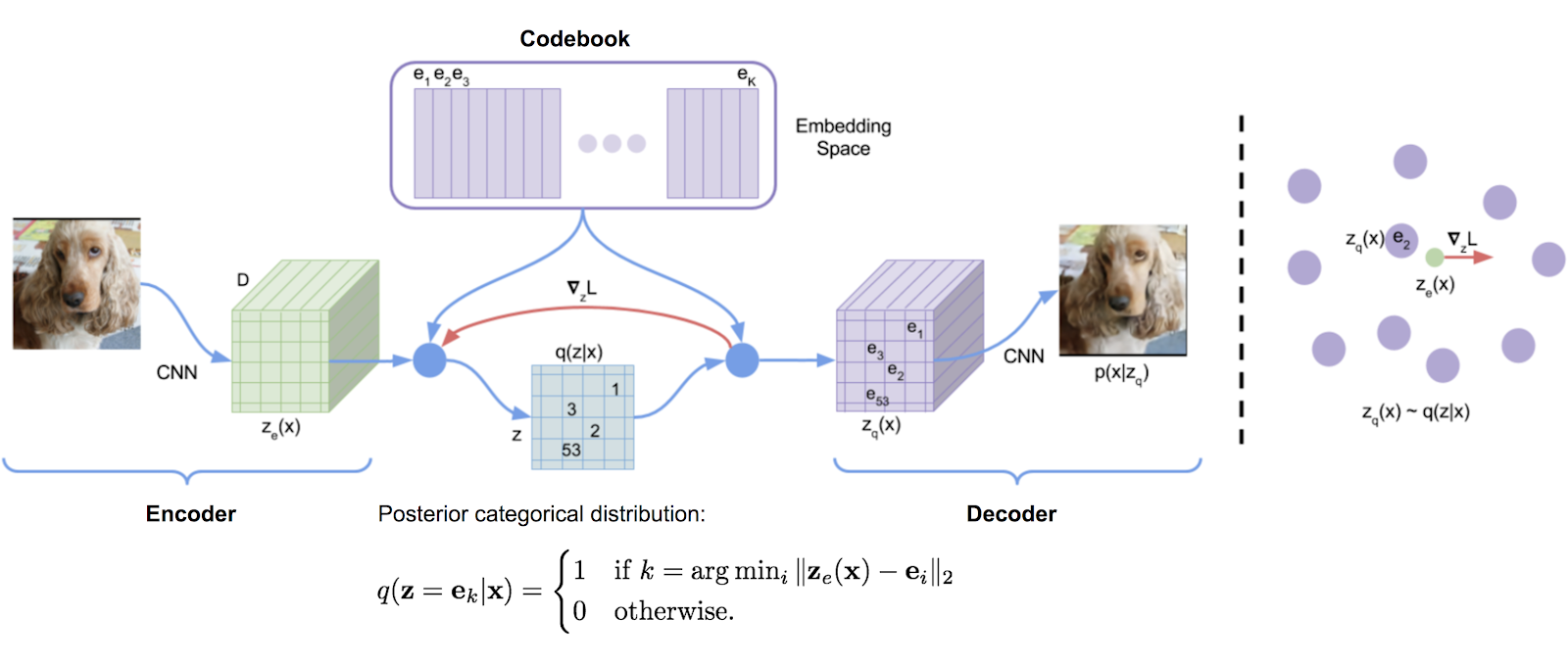
the encoder processes the image using a cnn produce a continuous latent representation $z_e(x)$, which serves as a mapping into the embedding space. the quantizer, $q(\cdot)$, discretizes this representation by mapping $z_e(x)$ to the nearest embedding vector $e_k$ in a learnable set of $k$ embedding vectors (right-hand side of figure). this results in a quantized representation $z_q(x)$, effectively enforcing a discrete and structured latent space. the decoder takes this quantized representation and passes it through another cnn to reconstruct the input, generating $p(x|z_q)$. the model is trained to minimize a compound perceptual and discriminative loss between the original image and $p(x|z_q)$.

multi-scale vqvae. identically to vqvae, the encoder produces a continuous feature map $z_e(x)$ using a cnn. however, instead of producing a single mapping of the same resolution as $z_e(x)$, the multi-scale vqvae iterates at produces $K$ token maps at different scales containing $h_k \times w_k$ tokens:

Loop through each scale $k$ (from the coarsest to the finest resolution):

1. Downsample the feature map $z_e(x)$ to $(h_k, w_k)$ using an interpolation function
2. Quantize the downsampled feature map using codebook $Z$ to obtain discrete token map $r_k$
3. Save token map to list $R$

So at each scale $k$ we get a token map of size $h_k \times w_k$ that points to a discrete vector in our codebook. After the vqvae has been fully trained, this is used as input to the VAR transformer. But, we need train the vqvae first, so how do we decode this representation? After we've collected the multi-scale token map $R$, we attempt to reconstruct the original image conditioned on our embedding space:

Loop through $R$ (from the coarsest to the finest resolution):

1. Retrieve $r_k$ (discrete tokens of shape $(h_k, w_k)$) from $R$
2. Lookup embeddings $z_k$ from codebook using $r_k$
3. Upsample $z_k$ to original image size $(h_K, w_K)$
4. Add reconstructed embeddings $z_k$ to $z_q$

The final step is then again to use the decoder on the quantized representation $z_q$ to reconstruct the image $p(x|z_q)$.

that's it. training this multi-scale vqvae will provides a way to generate the multi-scale token maps which are then used to train the VAR transformer. this method completely preserves the spatial locality of the image as scale encodes the entire image without a flattening process. Tokens in $r_k$ are fully correlated.

concluding thoughts

I can see why this paper won the best paper award, its such a clean proposition to a inherent problem of previous AR image modelling, it's intuitive, it aligns with the natural, coarse-to-fine progression characteristics of human visual perception, and the results speak for themselves. a couple of takeaways and things i found particularly interesting:

• eliminating inherent structure and minimizing assumptions scales better. this paper is yet another example in the long history of bitter lessons.
• the complexity of generating an image with VAR is orders of magnitude faster than previous AR methods thanks to the fact that $r_k$ represents an entire token map. Tokens in $r_k$ are fully correlated and you can generate tokens of each $r_k$ in parallel.
• the multi-scale VQVAE has a shared codebook across all scales. This is very surprising as it means the codebook needs to represent low and high level abstractions in the same space. It seems a considerable shift from what the codebook represents in a traditional VQVAE.
• how does this modelling scheme translate to other modalities? The paper suggests 3D images, but what about time series? or graphs?

hope you enjoyed.