Reading Roundup

Read some stuff over the past few days, don't have too much to say but wanted to share them anyway.

The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits

This paper from Microsoft has been making waves on Twitter as it's one of the first instances of successful 1-bit quantization-aware LLM training. The authors introduce a 1-bit LLM variant called BitNet b1.58, where every parameter is ternary, taking on values of {-1, 0, 1} ($\log_2(3) = 1.58$). Note that I say every parameter, this does not include activations, optimizer states and gradients. Still though, the fact that we can quantize weights into binaries is crazy. The performance of BitNet b1.58 matches Llama of equivalent size, while providing latency (1.67x - 4.10x), throughput(? - 8.9x) and memory (2.93x - 7.16x) improvements that scale with model size (1.3B - 70B). Another consequence of binarized networks is that matrix multiplications reduce to only addition.

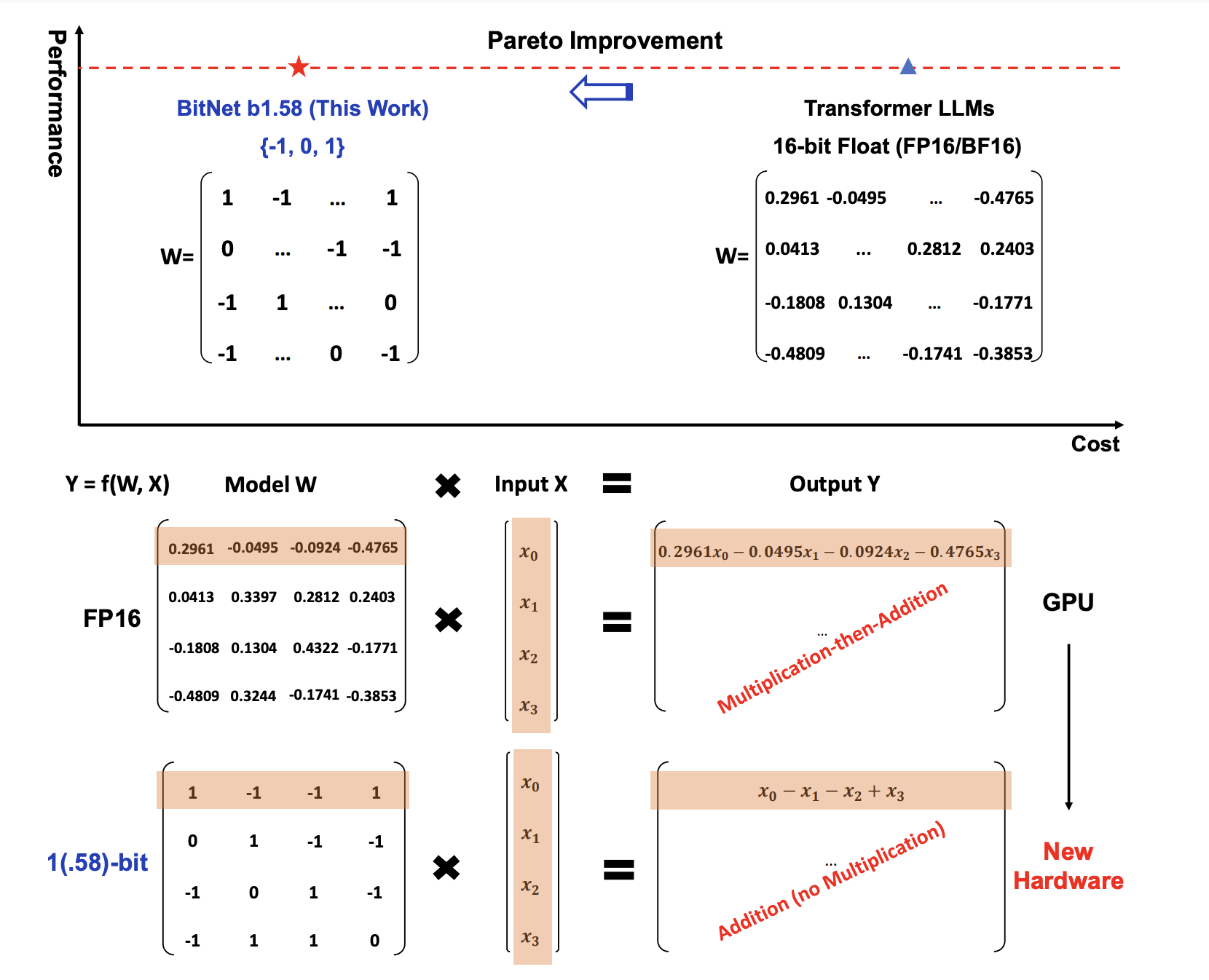
Most quantization techniques seem innocuous at first glance, but there are quite a few adjustments going on under the hood, which generally halt the adaptivity of such frameworks. BitNet has similar "issues" or "complications" that will most likely slow down its adaption. For example, they employ low-precision binary weights, but the activations are quantized, and the optimizer states + gradients are kept in high-precision. The binary weights are only introduced in the linear layers (pytorch nn.Linear). You can read more about the BitNet architecture in their original paper, link here.

Learning in High Dimension Always Amounts to Extrapolation

I was pretty excited for this paper, and it's certainly well written, but I was expecting more of a 'aa-ha' experience. They posed some interesting questions and demonstrations, but I couldn't really find a way to connect this to my own experiences. My takeaways are probably best illustrated by an excerpt from their Conclusion: Interpolation and extrapolation, as per Def. 1, provide an intuitive geometrical characterization on the location of new samples with respect to a given dataset. Those terms are commonly used as geometrical proxy to predict a model’s performances on unseen samples and many have reached the conclusion that a model’s generalization performance depends on how a model interpolates. In other words, how accurate is a model within a dataset’s convex-hull defines its generalization performances. In this paper, we proposed to debunk this (mis)conception. .... In short, the behavior of a model within a training set’s convex hull barely impacts that model’s generalization performance since new samples lie almost surely outside of that convex hull