Direct Preference Optimization: Your Language Model is Secretly a Reward Model

Nobody likes reinforcement learning. In theory it's all nice and clean but anyone who's working with RL practically (me, daily..) knows what a pain it is. Ever since RL became an integral part of LLM post-training alignment pipeline, researchers have been trying to do away with it. Despite it's intricacies, the RL fine-tuning stage has proven very sucessful in enabling LLMs to generalize to instructions beyond their instruction-tuning set and generally increase their usability. But... maybe not for much longer, the authors of this paper realize that the RL-based objective used by existing methods can be optimized exactly with a simple binary cross-entropy obective. This means that Direct Preference Optimization (DPO) optimizes a language model to adhere to human preferences, without explicit reward modeling or reinforcement learning!

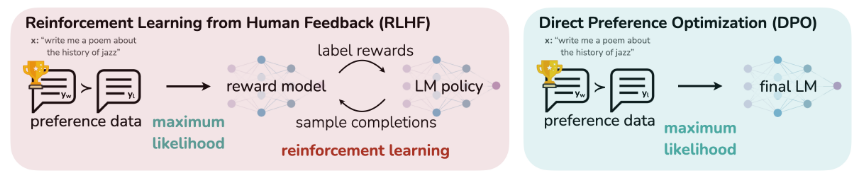
Traditional RLHF

Let's review the pipeline commonly used in RLHF.

SFT. The pre-trained model $\pi$ is fine-tuned using a supervised dataset of high-quality data, obtaining $\pi^{\text{SFT}}$.

Reward Modelling. The SFT model is prompted to produce pairs of answers $y_1, y_2, ...,y_n \sim \pi^{\text{SFT}}(y \mid x)$. The answers are then presented to human labelers who express preferences through ranking. It is common for $N = 2$ meaning that human labelers choose their preferred from two possible answers. One assumes that the preferences are generated by some latent reward model $r^*(y,x)$ which we don't have access to. To model this preference there are a number of possible choices, with the Bradely-Terry (BT) model being a popular one. The BT model stipulates that the human preference distribution $p^*$ can be written as:

$$p^*(y_1 \succ y_2 | x) = \frac{\exp(r^*(x, y_1))}{\exp(r^*(x, y_1)) + \exp(r^*(x, y_2))}.$$

A reward model $r_\phi(x,y)$ is used to parametrize the human preference rankings and its parameters are estimated via maximum likelihood. The model is initialized from the SFT model $\pi^{\text{SFT}}(y \mid x)$ with the addition of a linear layer head that transforms the $d_\text{model}$ output to a single scalar prediction for the reward value.

Reinforcement Learning. The learned reward model is used to provide preference feedback to the language model. Specifically, one models the following optimization problem

$$\max_{\pi_\theta} \mathbb{E}_{x \sim D,y \sim \pi_\theta(y \mid x)} \left[ r_\phi(x, y) \right] - \beta \mathrm{D}_{\mathrm{KL}} \left[ \pi_\theta(y \mid x) \mid\mid \pi^{\text{SFT}}(y \mid x) \right].$$

In practice, the language model policy $\pi_\theta$ is initialized from $\pi^{\text{SFT}}$, where the rate of deviation between the two is controlled by weighting the Kullback-Leibler divergence term, $\beta \mathrm{D}_{\mathrm{KL}}$. Intuitively we can imagine the policy trying to maximize the reward while regulating our policy divergence. The objective is not differentiable and is typically optimized with reinforcement learning by maximizing the following reward function using PPO:

$$r(x, y) = r_\phi(x, y) - \beta(\log \pi_\theta(y \mid x) - \log \pi^{\text{SFT}}(y \mid x)).$$

Direct Preference Optimization

The goal of DPO is to derive a simple approach for policy optimization using preferences directly, removing the reward model middleman and RL optimization. Where RLHF learns a reward model and optimizes for it via RL, DPO leverages a particular choice of reward model parameterization that enables direct extraction of the final optimal policy $\pi^*_\theta(y \mid x)$. The key insight is leveraging an analytical mapping from reward functions to optimal policies, which enables the transformation of a reward model loss function into a loss function over policies. This clever trick avoids fitting an explicit, standalone reward model, while still optimizing under existing models of human preference.

The exact derivations can be found in the paper, Section 4, Appendix A.1 and Appendix A.2. To capture the essence of the derivations we go back to the preference model we established earlier

$$p^*(y_1 \succ y_2 \mid x) = \frac{\exp(r^*(x, y_1))}{\exp(r^*(x, y_1)) + \exp(r^*(x, y_2))}.$$

Notice how the model is a function of the reward model, now imagine if we were instead able to model this as a function of the policies. The authors realize that such a reformulation is possible analytically, deriving a probability of human preference data in terms of only the optimal policy $\pi*$ and reference policy $\pi^{\text{SFT}}$:

$$p^*(y_1 \succ y_2 \mid x) = \frac{1}{1 + \exp(\beta \log \frac{\pi^*(y_2\mid x)}{\pi^{\text{SFT}}(y_2\mid x)} - \beta \log \frac{\pi^*(y_1\mid x)}{\pi^{\text{SFT}}(y_1\mid x)})}.$$

In the end what this means is that one can formulate a simple maximum likelihood objective over human preference data w.r.t a parametrized policy $\pi_\theta$ and a reference policy $\pi^{\text{SFT}}$, completely removing the need for a explicit reward model and RL! Given a sample $(x, y_l, y_w)$, the DPO update rule increases the likelihood of the preferred completion $y_w$ and decreases the likelihood of dispreferred completions $y_l$. Importantly, the examples are weighed by how much higher the implicit reward model $\beta \log \frac{\pi_\theta(y\mid x)}{\pi^{\text{SFT}}(y\mid x)}$ rates the dispreferred completions, scaled by how incorrectly the implicit reward model orders the completions.

DPO vs IPO vs KTO

DPO's success has prompted the exploration of new loss functions, focusing on two lacking aspects of DPO:

• Robustness. One shortcoming of DPO is that it is prone to overfit on the preference dataset if you aren't ready to perform early stopping. As a response to this, DeepMind published Identity Preference Optimization, which adds a regularizing term ot the DPO loss.
• Paired preference data. Alignment methods typically requires paired preference data $(x, y_w, y_l)$ and DPO is no different. Collecting this kind of data is, as we've repeated consistently, expensive and time consuming. Kahneman-Taversky Optimization reformulates the loss function such that it depends entirely on individual examples that have been labeled as good or bad. These are much easier to acquire in practice.

A team at huggingface recently published a comparison of these three alignment methods, evaluating their performance across a range of different $\beta$ values. I found this post to be super interesting so I'd like to share the results with you. The team aligned two SFT models: OpenHermes-2.5-Mistral-7B and Zephyr-7B-Beta, results below.

Zephyr clearly benefits from a small $\beta$, where DPO is the strongest performer. However, across the spectrum it's actually KTO that wins. On OpenHermes-Mistral the results are way less satisfying, overall however it seems that DPO > KTO > IPO with the $\beta$ sweet spot alternating for each algorithm.

Final thoughts

It's fairly rare to see such an innovative analytical derivation that omits entire steps of a learning pipeline. RLHF is inherently a very brittle process that most of the open-source community has failed to adopt seamlessly. DPO appears to make this process a lot more robust and it's taken over as the preferred fine-tuning step following SFT. Unfortunately, this still requires human preference data which can be expensive to obtain but synthetic data is becoming more and more prominent in that regard. To finish off I reiterate the beautiful title statement: Your Language Model is Secretly a Reward Model