Mastering the Game of Stratego with Model-Free Multiagent Reinforcement Learning

Progress in AI has long been measured by its performance on different board games. Among those Stratego has for a long time been considered the next frontier of AI research. Solutions which require minimal prior knowledge are of particular interest because they open up avenues for expansion beyond that of the isolated gameboard. I recently read about ReBeL, where researchers where able to solve 2 player Poker using only self-player and no prior domain knowledge. Today, we're covering an algorithm capable of human expert level performance on games of previously uncomparable scale.

A Game Theorist's approach to DeepRL

ReBeL adopted the AlphaZero recipe for imperfect-information games creating an agent that achieves superhuman performance on heads-up no-limit Texas hold'em with minimal domain knowledge. The RL + Search framework, established in AlphaZero, was generalized to converge to a Nash equilibrium in all two-player zero-sum games, reducing to an algorithm similar to AlphaZero in the perfect information scenario. The critical element of ReBeL's imperfect information RL + Search framework is the expanded notion of state to include not only the current state and action history but also the common-knowledge belief distribution over states, which is determined by the public observations shared by all agents and the policy of all agents. While it might be tempting to apply this framework to Stratego, the complexity of the games are not comparative. Stratego has a game tree complexity $10^{170}\times$ larger than Go, more starting configurations than Poker by a factor of $10^{60}$, and many more turns (in a game) than any previously solved games. Search is no longer feasible.

Instead, DeepNash proposes a model-free reinforcement learning algorithm - ignoring an explicit belief space to track and model what the opponent is doing. DeepNash focuses entirely on its own play to converge to a Nash equilibrium. In the Nash equilibrium, each player's strategy is optimal when considering the decisions of other players. It means that a player has 50% change of winning, when playing against a player of equal skill. Intuitively, the idea is to focus on self-play to develop unexploitable strategies for the opponent.

A Stratego observation

DeepNash scales the R-NaD algorithm using deep learning architectures, in ways that is reminiscent of previous work we've covered. The neural network is input with a encoded observation tensor consisting of player pieces, public information, game phase and the past 40 actions. The representation is depicted in the figure below.

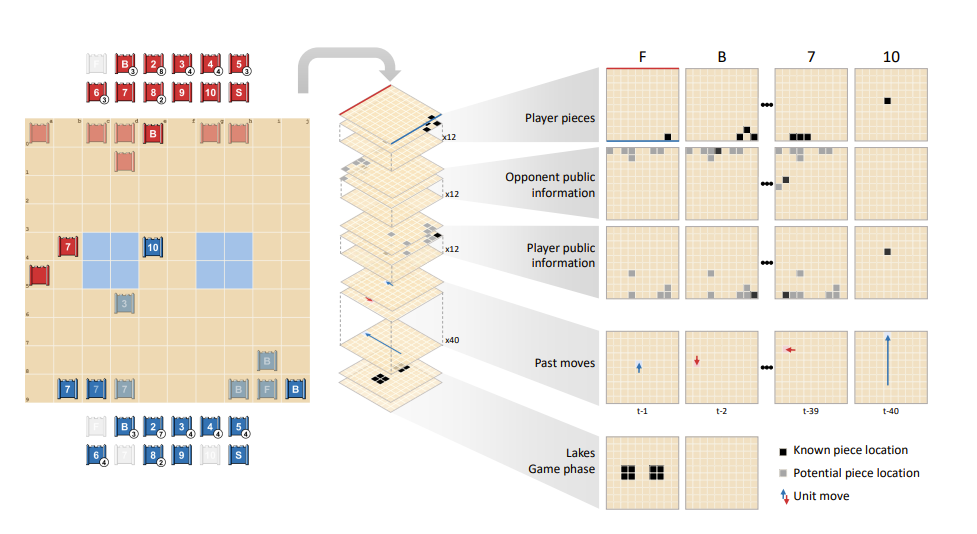
Notice how similar this is to the representation of Go, Chess and Shogi in AlphaZero. Encoding pieces, public state information and action history using sparse matrixes is robust and flexible, enabling spatial information flow within the network. For those interested, the rest of the neural network is depicted in the Supplementary Material. The observation passes through a residual neural network, structured as a U-Net, to four heads generating output of appropriate shape. Three of these heads output probability distributions of actions i.e policies, and the last one is a value head which outputs a scalar. The different policies represent three distinct game phases: deployment of pieces, selection of next piece and action of next piece.

Regularized Nash Dynamics

The R-Nad learning algorithm used in DeepNash has roots in evolutionary game theory and is based on the idea of regularization for convergence. Unfortunately, the description of the process and how it integrates with self-play + neural network training is hazy and in my opinion quite difficult to grasp. The authors mention that it is possible to define a learning update rule that induces a dynamical system for which there exists a so-called Lyapunov function. This function converges to a fixed point which may or may not be a nash equilibrium. This fixed point is used as the regularization policy for a new iteration and apparently if you perform this iteratively it is proven to converge to a nash equilibrium. I'd love to understand more about how this process ties in with self-play, how the neural network is used and when/how it is updated. Hoping I can find a more intuitive explanation of R-Nad and come back to this post.