Deep Double Descent: Where Bigger Models and More Data Hurt

I was listening to a podcast recently with one of the co-authors of this paper, Ilya Sutskever, and he briefly mentioned this paper. Looking it up I was thrilled to learn that it tackles a general Deep Learning phenomena rather than just being a NLP paper, which I've been reading a lot of recently. Coming from more of a statistical machine learning background, this paper really hits on one of the overarching questions I've had when reading LLM papers. Why are none of them exhibiting overfitting behavior? Overfitting is a fundamental problem in a lot of deep learning applications and it's something I've had to tangle with on numerous occasions meanwhile we seem to be able to endlessly scale Transformer models without even thinking about this central problem. Along with that the authors more "conventional wisdoms" about neural networks discussing things such as the bias/variance tradeoff, model scale, data scale and training/test performance.

Effective Model Complexity

Double descent is a phenomena that was first theorized in 2018 where it was demonstrated for decision trees, random features, and 2 layer neural networks. The authors build upon this work by showing that double descent is a robust phenomena that occurs in a variety of deep learning tasks, architectures and optimization methods. More generally they find that deep learning settings have two regimes: In the under-parametrized regime where model complexity is small compared to the number of samples, the test error behaves in a U-like manner as predicted by the classical bias/variance tradeoff. However, given sufficient model complexity, increasing model complexity only decreases test error, following the modern intuition of bigger models are better. In combination these behaviors give life to the double descent phenomena.

This is however not sufficient in explaining the entire picture behind double descent and they need a more general notion of the phenomena, that goes beyond varying the number of parameters. For this purpose, the authors define effective model complexity (EMC) of a training procedure as the maximum number of samples on which it can achieve close to zero training error. Together with this definition they present an hypothesis that learning algorithms experience double descent as a function of EMC rather than just model parameters. They observe both "epoch-wise double descent" and "model-wise double descent" to support this hypothesis. The figure below demonstrates this perfectly.

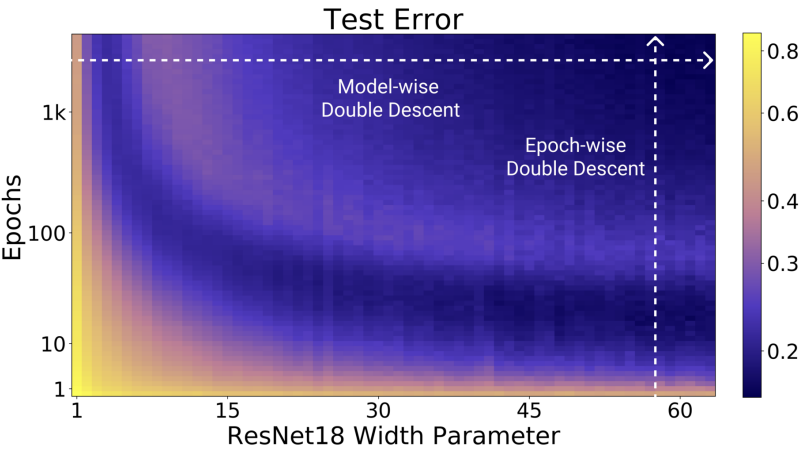
Additionally the authors provide an informal hypothesis regarding double descent, this is taken directly from the paper:

Important to note here is that EMC is a function of training procedure, data distribution and model architecture. Although the reasons behind double descent remains uncertain, the authors provide substantial experiments to conclude the robustness of its occurrence along with some discussions, which I'll walk through next.

Model-wise Double Descent

This phenomena is observed consistently throughout different architectures, optimizers and datasets when varying model size (with constant optimization steps). The experiments also find that any modifications which increase the interpolation threshold, such as adding noise, using data augmentation, and increasing the number of train samples corresponds to a shift of the peak in test error towards larger models. This implies that there is a crucial interval around the interpolation threshold when EMC = n; below and above this interval increasing complexity helps performance, while within this interval it may hurt performance.

As I mentioned, the authors clearly state that there is no theoretical understanding of this phenomena but they do provide some helpful intuition which, to me at least, proves satisfying. Okay, so for model-sizes (remember we are in the model-wise double descent scenario here) in the critical interval around the interpolation threshold there is effectively one model that fits the train data and this model becomes very sensitive to noise in the training set. Since its barely able to fit the train data, forcing it to fit even slightly noisy data will destroy its global structure resulting in a high test error. This theory is supported by the fact that ensembling helps significantly in the critical parametrized regime. In the over-parametrized setting, there are many models which fit the data and as such SGD is able to find one that absorbs the noise while still performing well on the distribution.

Epoch-wise Double Descent

In addition to the model-wise double descent, the authors demonstrate a novel form of double descent with respect to training epochs which is in line with the suggestion that the phenomena is a function of EMC. Increasing the training time increases the EMC and thus sufficiently large models transition from under- to over-parametrized over the course of training. It's important to note that this behavior requires sufficiently large models to occur. This is best illustrated using a figure directly form the paper, shown below.

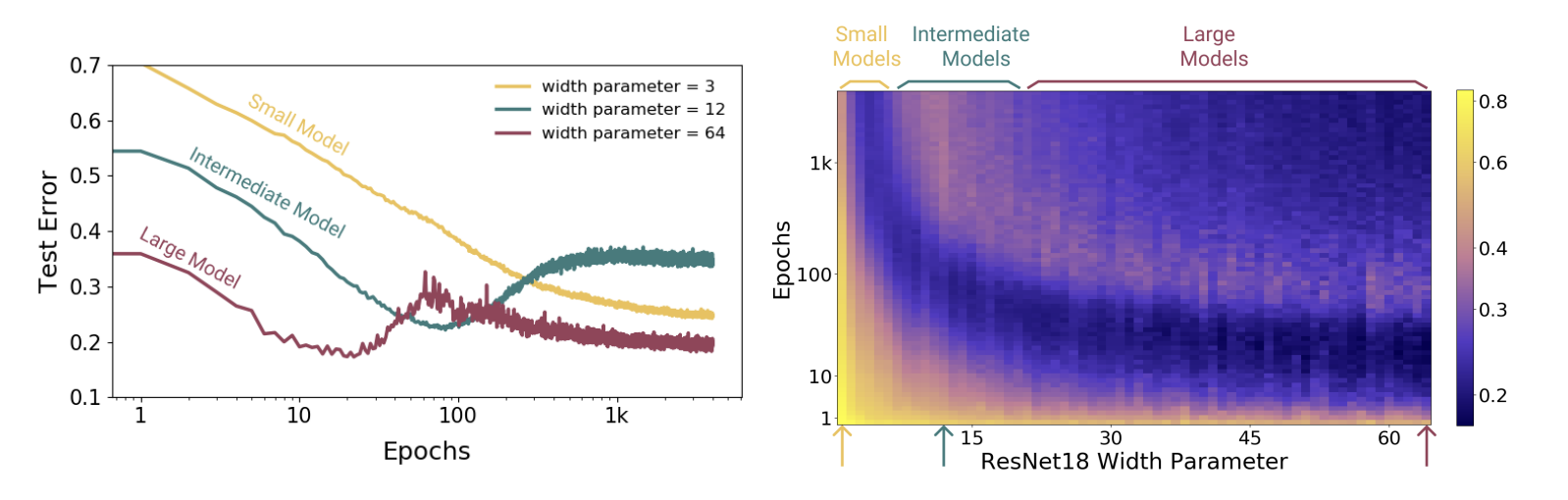
Final Thoughts

I think this is a very intriguing paper and I'm really glad that I stumbled upon something that tackles such a central part of all deep learning applications. It's clear how much of deep learning still remains an open question, and how empirical-central this field is as opposed to something like the physics which is almost purely driven by well executed theoretical hypothesis. Anyway I hope I can make use of the intuitions provided by the authors in my future work, sometimes it's hard to make use of everything I read but I'm going to try to make this one stick.